배경
무작위배정은 임상시험에서 편향을 차단하고 타당한 통계적 추론을 가능하게 하는 핵심 장치다. 그러나 소표본 (전형적 2상, 중간분석 혹은 소집단 분석)이거나, 치료군 수가 많거나 층화요인이 많아서 집단이 다수로 분할되는 상황에서는, 어떤 배정 설계를 택하느냐가 군간 불균형과 검정력 (power)에 직접적인 영향을 준다.
본 글은 전통적으로 쓰이는 설계 (단순무작위배정, 순열블록, 층화, 층화+순열블록)를 간단히 요약하고, MSB (minimal sufficient balance) 방식을 소개한다.
단순무작위배정 (Simple randomization)
단순무작위배정의 개념을 그림 1에 도시하였다.
단순무작위배정은 배정 은닉(allocation concealment)과 예측 불가능성 측면에서 가장 이상적이다. 다만 소표본에서는 우연한 군간 불균형이 잦다. 예를 들어 총 40명(군당 20명 배정 계획)이 참여하는 2군 시험에서 군간 표본수가 20% 이상 벌어질 확률은 대략 25–30%로 알려져 있으며, 이런 불균형은 결국 검정력 저하로 이어진다. 검정력은 각 치료군에 배정된 대상자 수가 같을 때 가장 높으며, 불균형의 정도가 커질수록 검정력이 낮아지기 때문이다.
▲ 그림 1. Simple randomization
순열블록 무작위배정 (Permuted block randomization)
순열블록 무작위배정의 개념을 그림 2에 도시하였다.
순열블록 (permuted block)은 블록 단위 (예: 블록 크기 4 → A 2명, B 2명)로 배정하여, 블록이 완결될 때마다 주기적으로 균형을 보장한다. 중간분석이나 조기 종료가 있어도 전체 균형을 일정 부분 (미완성 블록의 수가 적다면) 유지한다는 장점이 있다.
하지만 공개 (open-label) 임상시험에서 작은 블록을 쓰면 다음 배정이 예측 가능해져 선택 편향(selection bias) 위험이 커진다. 또한 기관 수가 많거나 블록 크기를 크게 하거나, 기관별 블록을 적용할 경우 블록별 등록 부족으로 마지막 블록이 미완성 (불완전 블록)으로 남기 쉽고, 블록 구조의 제약이 분석을 복잡하게 만들어 검정력과 효율을 떨어뜨릴 수 있다. 더욱이 설령 대상자 수의 균형을 달성한 경우에도, 결과에 영향을 미치는 중요한 예후 요인의 불균형이 생기면 편향된 임상시험 결과를 초래할 수 있다.
▲ 그림 2. Permuted Block Randomization
층화 무작위배정 (Stratified randomization)
층화 무작위배정의 개념을 그림 3에 도시하였다.
치료군에 대한 무작위배정을 각 층화 요인 별로 실시하는 배정법이다. 층화는 중요한 예후 인자 (예: 임상시험실시기관, 성별, 중증도 등)가 처치군과 대조군에 균등하게 분포하도록 돕는다. 소규모 시험에서 단순무작위배정을 사용하면 중요한 예후 인자의 불균형이 생길 수 있는데, 층화는 이를 줄여 타당성과 신뢰성을 높인다.
다만 층화 변수를 많이 사용하면 전체 층 (strata) 수가 기하급수적으로 늘 수 있으므로 (예 남녀 2, 중증도 3이라면 총 6개) 각 층에 배정되는 표본수가 매우 적거나 아예 모집이 되지 않을 수 있다. 이 경우 층화의 이점이 현실적으로 구현되지 못한다.
또한 대상자가 무작위배정 전에 모든 층화 요인을 알지 못하면 층화 무작위배정 자체가 불가능하다.
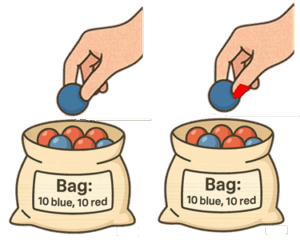
▲ 그림 3. Stratified randomization
층화 순열블록 무작위배정 (Stratified permuted block randomization)
가장 빈번히 사용되고 있는 층화 순열불록 무작위배정의 개념을 그림 4에 도시하였다.
층화와 순열블록을 결합해 각 층 내에서 블록을 운영하면, 이론적으로 층별 표본수 균형을 정밀하게 확보할 수 있다. 예후성이 강한 소수의 층화요인을 선정하고, 분석에서도 해당 층화요인을 고정효과로 포함하면 잔차분산 (residual variance)이 줄어 검정력 유지 및 향상을 기대할 수 있다.
문제는 층화 순열블록 무작위배정은 실시기관(site)과 층(strata) 수가 증가할수록 실시기관×층의 블록이 급증 (과층화 (over-stratification))으로 인하여 소표본·다층화 환경에서는 불완전 블록과 희소층이 층화와 블록 중 하나만을 적용할 때보다 더 쉽게 생겨, 층화와 블록의 단점이 가중될 수 있다.
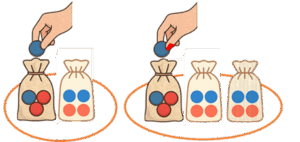
▲ 그림 4. Stratified permuted block randomization
MSB(minimal sufficient balance): 무작위성 유지 + 최소 개입 균형
MSB의 개념을 도시하는 것은 쉽지 않다. 사전에 정한 임계치를 넘을 때 배정 확률을 불균형 완화 방향으로 기울인다 점을 구부러진 동전에 비유하여 그림 5에 도시하였다.
MSB는 기존 배정된 사람들의 누적된 공변량 정보를 평가하여 공변량의 전체 균형에 유리하도록 새롭게 도착한 환자의 배정을 하는 동적 무작위 배정(Adaptive Randomization) 방식이다. 불균형 정도가 임계치 미만이면 동전던지기 (2군일 경우 50%: 50%) 수준으로 무작위성을 최대한 유지하다가, 불균형의 정도가 사전에 정한 임계치를 넘을 때에만 배정 확률을 불균형 완화 방향 (biased coin)으로 살짝 기울인다. 이러한 최소 개입의 특성을 반영해 minimal sufficient balance라고 부른다.
MSB는 블록처럼 강제로 맞추지 않기 때문에 예측 가능성이 낮고, 블록을 채워야 하는 제약이 없어 중간 종료·불균등 등록에 유연하다. 또한 층을 과도하게 세분하지 않고도 다수 공변량의 전반적 불균형을 제어할 수 있어, 소표본·다공변량 환경에서 잔차분산의 불필요한 팽창을 억제하고 검정력 손실을 최소화하는 장점이 있다.
결과적으로 MSB는 전통적으로 사용되어 온 무작위배정 방식의 한계점들을 보완해, 무작위성은 보존하면서 의미 있는 불균형만 최소화하도록 설계된 방식이다.
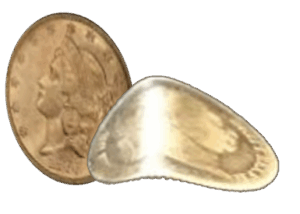
▲ 그림 5. MSB (using Biased coin)
결론
소표본·다층화 환경에서 과층화로 인한 불완전 블록과 희소층 발생 위험은 결과적으로 검정력을 감소시킬 수 있다. 따라서 현 시점에서 빈번히 사용되고 있는 설계 (단순무작위배정, 순열블록, 층화, 층화+순열블록)는 2상이나 희귀질환 등 소규모 임상시험에서 유용성이 제한적이다.
추가적으로, 각 기관 별로 특정 치료군으로 쏠림이 단기적으로 발생해 임상시험용의약품 재고 운영이 일시적으로 출렁일 수 있다.
MSB는 무작위성을 희생하지 않으면서 필요한 순간에만 최소 개입으로 균형을 보완해 검정력 손실을 줄이는 실용적 대안이다.
2상은 유망 후보를 선별하는 단계이므로, 효과가 있는 약물을 놓치지 않는 것이 중요하다. 이 관점에서, 검정력을 불필요하게 낮출 수 있는 배정 방식은 지양되고, MSB 무작위배정이 눈가림·공개 시험 모두에서 합리적 선택지로 평가될 수 있다.
결론적으로 그림 6에 요약하였듯이, 적용법 (implementation)이 다소 어려운 단점이 있지만, 여러 무작위배정 방법 중 무작위성 유지 (allocation randomness), 배정목적 달성 (target allocation), 다치료군 적용 (number of arms), 기저 공변량 관련 유연성 (baseline covariates type과 number) 측면 등을 종합적으로 고려하였을 때 가장 우월한 무작위배정법으로 판단된다.
심유의 IWRS는 여러 무작위배정 방식이 구동 가능하며, MSB 방식도 선택 가능하다.
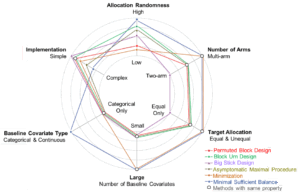
▲ 그림 6. 무작위 배정방법의 상대적 장단점 (Relative pros and cons of randomization methods)
그림 6 출전: Stroke. 2023 Jul;54(7):1909-1919. doi: 10.1161/STROKEAHA.122.040743.
Biostatistics and Biometrics Team